7  Regression II

7.1 Concepts

The Regression Line

The regression line is fitted so that the average distance between the line and the sample points is as small as possible. The line is defined by a slope (\(\beta\)) and an intercept (\(\alpha\)). Mathematically, the regression line is expressed as \(\hat{y_i}=\hat{\alpha}+\hat{\beta}x_i\), where \(\hat{y_i}\) are the predicted values of \(y\) given the \(x\)’s.

  • The slope determines the steepness of the line. The estimate quantifies how much a unit increase in \(x\) changes \(y\). The estimate is given by \(\hat{\beta}= \frac {s_{xy}}{s_{x}^2}\).

  • The intercept determines where the line crosses the \(y\) axis. It returns the value of \(y\) when \(x\) is zero. The estimate is given by \(\hat{\alpha}=\bar{y}-\hat{\beta}\bar{x}\).

Goodness of Fit

There are a couple of popular measures that determine the goodness of fit of the regression line.

  • The coefficient of determination or \(R^2\) is the percent of the variation in \(y\) that is explained by changes in \(x\). The higher the \(R^2\) the better the explanatory power of the model. The \(R^2\) is always between [0,1]. To calculate use \(R^2=SSR/SST\).

    • \(SSR\) (Sum of Squares due to Regression) is the part of the variation in \(y\) explained by the model. Mathematically, \(SSR=\sum{(\hat{y_i}-\bar{y})^2}\).

    • \(SSE\) (Sum of Squares due to Error) is the part of the variation in \(y\) that is unexplained by the model. Mathematically, \(SSE=\sum{(y_i-\hat{y_i})^2}\).

    • SST (Sum of Squares Total) is the total variation of \(y\) with respect to the mean. Mathematically, \(SST=\sum{(y_i-\bar{y})^2}\).

    • Note that \(SST=SSR+SSE\).

  • The adjusted \(R^2\) recognizes that the \(R^2\) is a non-decreasing function of the number of explanatory variables in the model. This metric penalizes a model with more explanatory variables relative to a simpler model. It is calculated by \(1-(1-R^2) \frac {n-1}{n-k-1}\), where \(k\) is the number of explanatory variables used in the model and \(n\) is the sample size.

  • The Residual Standard Error estimates the average dispersion of the data points around the regression line. It is calculated by \(s_e =\sqrt{\frac{SSE}{n-k-1}}\).

Useful R Functions

The lm() function to estimates the linear regression model.

The predict() function uses the linear model object to predict values. New data is entered as a data frame.

The coef() function returns the model’s coefficients.

The summary() function returns the model’s coefficients, and goodness of fit measures.

7.2 Exercises

The following exercises will help you get practice on Regression Line estimation and interpretation. In particular, the exercises work on:

  • Estimating the slope and intercept.

  • Calculating measures of goodness of fit.

  • Prediction using the regression line.

Answers are provided below. Try not to peak until you have a formulated your own answer and double checked your work for any mistakes.

Exercise 1

For the following exercises, make your calculations by hand and verify results using R functions when possible.

  1. Consider the data below. Calculate the deviations from the mean for each variable and use the results to estimate the regression line. Use R to verify your result. On average by how much does y increase per unit increase of x?
x 20 21 15 18 25
y 17 19 12 13 22

  1. Calculate SST, SSR, and SSE. Confirm your results in R. What is the \(R^2\)? What is the Standard Error estimate? Is the regression line a good fit for the data?

  2. Assume that x is observed to be 32, what is your prediction of y? How confident are you in this prediction?

Exercise 2

You will need the Education data set to answer this question. You can find the data set at https://jagelves.github.io/Data/Education.csv . The data shows the years of education (Education), and annual salary in thousands (Salary) for a sample of \(100\) people.

  1. Estimate the regression line using R. By how much does an extra year of education increase the annual salary on average? What is the salary of someone without any education?

  2. Confirm that the regression line is a good fit for the data. What is the estimated salary of a person with \(16\) years of education?

Exercise 3

You will need the FoodSpend data set to answer this question. You can find this data set at https://jagelves.github.io/Data/FoodSpend.csv .

  1. Omit any NA’s that the data has. Create a dummy variable that is equal to \(1\) if an individual owns a home and \(0\) if the individual doesn’t. Find the mean of your dummy variable. What proportion of the sample owns a home?

  2. Run a regression with Food being the dependent variable and your dummy variable as the independent variable. What is the interpretation of the intercept and slope?

  3. Now run a regression with Food being the independent variable and your dummy variable as the dependent variable. What is the interpretation of the intercept and slope? Hint: you might want to plot the scatter diagram and the regression line.

Exercise 4

You will need the Population data set to answer this question. You can find this data set at https://jagelves.github.io/Data/Population.csv .

  1. Run a regression of Population on Year. How well does the regression line fit the data?

  2. Create a prediction for Japan’s population in 2030. What is your prediction?

  3. Create a scatter diagram and include the regression line. How confident are you of your prediction after looking at the diagram?

7.3 Answers

Exercise 1

  1. The regression lines is \(\hat{y}=-4.93+1.09x\). For each unit increase in x, y increases on average \(1.09\).

Start by generating the deviations from the mean for each variable. For x the deviations are:

x<-c(20,21,15,18,25)
(devx<-x-mean(x))
[1]  0.2  1.2 -4.8 -1.8  5.2

Next, find the deviations for y:

y<-c(17,19,12,13,22)
(devy<-y-mean(y))
[1]  0.4  2.4 -4.6 -3.6  5.4

For the slope we need to find the deviation squared of the x’s. This can easily be done in R:

(devx2<-devx^2)
[1]  0.04  1.44 23.04  3.24 27.04

The slope is calculated by \(\frac{\sum_{i=i}^{n} (x_{i}-\bar{x})(y_{i}-\bar{y})}{\sum_{i=i}^{n} (x_{i}-\bar{x})^2}\). In R we can just find the ratio between the summations of (devx)(devy) and devx2.

(slope<-sum(devx*devy)/sum(devx2))
[1] 1.087591

The intercept is given by \(\bar{y}-\beta(\bar{x})\). In R we find that the intercept is equal to:

(intercept<-mean(y)-slope*mean(x))
[1] -4.934307

Our results can be easily verified by using the lm() and coef() functions in R.

fitEx1<-lm(y~x)
coef(fitEx1)
(Intercept)           x 
  -4.934307    1.087591
  1. SST is \(69.2\), SSR is \(64.82\) and SSE is \(4.38\) (note that \(SSR+SSE=SST\)). The \(R^2\) is just \(\frac{SSR}{SST}=0.94\) and the Standard Error estimate is \(1.21\). They both indicate a great fit of the regression line to the data.

Let’s start by calculating the SST. This is just \(\sum{(y_{i}-\bar{y})^2}\).

(SST<-sum((y-mean(y))^2))
[1] 69.2

Next, we can calculate SSR. This is calculated by the following formula \(\sum{(\hat{y_{i}}-\bar{y})^2}\). To obtain the predicted values in R, we can use the output of the lm() function. Recall our fitEx1 object created in Exercise 1. It has fitted.values included:

(SSR<-sum((fitEx1$fitted.values-mean(y))^2))
[1] 64.82044

The ratio of SSR to SST is the \(R^2\):

(R2<-SSR/SST)
[1] 0.9367115

Finally, let’s calculate SSE \(\sum{(y_{i}-\hat{y_{i}})^2}\):

(SSE<-sum((y-fitEx1$fitted.values)^2))
[1] 4.379562

With the SSE we can calculate the Standard Error estimate:

sqrt(SSE/3)
[1] 1.208244

We can confirm these results using the summary() function.

summary(fitEx1)

Call:
lm(formula = y ~ x)

Residuals:
      1       2       3       4       5 
 0.1825  1.0949  0.6204 -1.6423 -0.2555 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)   
(Intercept)  -4.9343     3.2766  -1.506  0.22916   
x             1.0876     0.1632   6.663  0.00689 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.208 on 3 degrees of freedom
Multiple R-squared:  0.9367,    Adjusted R-squared:  0.9156 
F-statistic:  44.4 on 1 and 3 DF,  p-value: 0.00689
  1. If \(x=32\) then \(\hat{y}=29.87\). The regression is a good fit, so we can feel good about our prediction. However, we would be concerned about the sample size of the data.

In R we can obtain a prediction by using the predict() function. This function requires a data frame as an input for new data.

predict(fitEx1, newdata = data.frame(x=c(32)))
       1 
29.86861

Exercise 2

  1. An extra year of education increases the annual salary about \(5,300\) dollars (slope). A person that has no education would be expected to earn \(17,2582\) dollars (intercept).

Start by loading the data in R:

Education<-read.csv("https://jagelves.github.io/Data/Education.csv")

Next, let’s use the lm() function to estimate the regression line and obtain the coefficients:

fitEducation<-lm(Salary~Education, data = Education)
coefficients(fitEducation)
(Intercept)   Education 
  17.258190    5.301149
  1. The \(R^2\) is \(0.668\) and the standard error is \(21\). The line is a moderately good fit. If someone has \(16\) years of experience, the regression line would predict a salary of \(102,000\) dollars.

Let’s get the \(R^2\) and the Standard Error estimate by using the summary() function and fitEx1 object.

summary(fitEducation)

Call:
lm(formula = Salary ~ Education, data = Education)

Residuals:
    Min      1Q  Median      3Q     Max 
-62.177  -9.548   1.988  15.330  45.444 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  17.2582     4.0768   4.233  5.2e-05 ***
Education     5.3011     0.3751  14.134  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 20.98 on 98 degrees of freedom
Multiple R-squared:  0.6709,    Adjusted R-squared:  0.6675 
F-statistic: 199.8 on 1 and 98 DF,  p-value: < 2.2e-16

Lastly, let’s use the regression line to predict the salary for someone who has \(16\) years of education.

predict(fitEducation, newdata = data.frame(Education=c(16)))
       1 
102.0766

Exercise 3

  1. Approximately, \(36\)% of the sample owns a home.

Start by loading the data into R and removing all NA’s:

Spend<-read.csv("https://jagelves.github.io/Data/FoodSpend.csv")
Spend<-na.omit(Spend)

To create a dummy variable for OwnHome we can use the ifelse() function:

Spend$dummyOH<-ifelse(Spend$OwnHome=="Yes",1,0)

The average of the dummy variable is given by:

mean(Spend$dummyOH)
[1] 0.3625
  1. The intercept is the average food expenditure of individuals without homes (\(6417\)). The slope, is the difference in food expenditures between individuals that do have homes minus those who don’t. We then conclude that individuals that do have a home spend about \(-2516\) less on food than those who don’t have homes.

To run the regression use the lm() function:

lm(Food~dummyOH,data=Spend)

Call:
lm(formula = Food ~ dummyOH, data = Spend)

Coefficients:
(Intercept)      dummyOH  
       6473        -3418
  1. The scatter plot shows that most of the points for home owners are below \(6000\). For non-home owners they are mainly above \(6000\). The line can be used to predict the likelihood of owning a home given someones food expenditure. The intercept is above one, but still it gives us the indication that it is likely that low food expenditures are highly predictive of owning a home. The slope tells us how that likelihood changes as the food expenditures increase by 1. In general, the likelihood of owning a home decreases as the food expenditure increases.

Run the lm() function once again:

fitFood<-lm(dummyOH~Food,data=Spend)
coefficients(fitFood)
  (Intercept)          Food 
 1.4320766616 -0.0002043632

For the scatter plot use the following code:

plot(y=Spend$dummyOH,x=Spend$Food, 
     main="", axes=F, pch=21, bg="blue",
     xlab="Food",ylab="Dummy")
axis(side=1, labels=TRUE, font=1,las=1)
axis(side=2, labels=TRUE, font=1,las=1)
abline(fitFood,
       col="gray",lwd=2)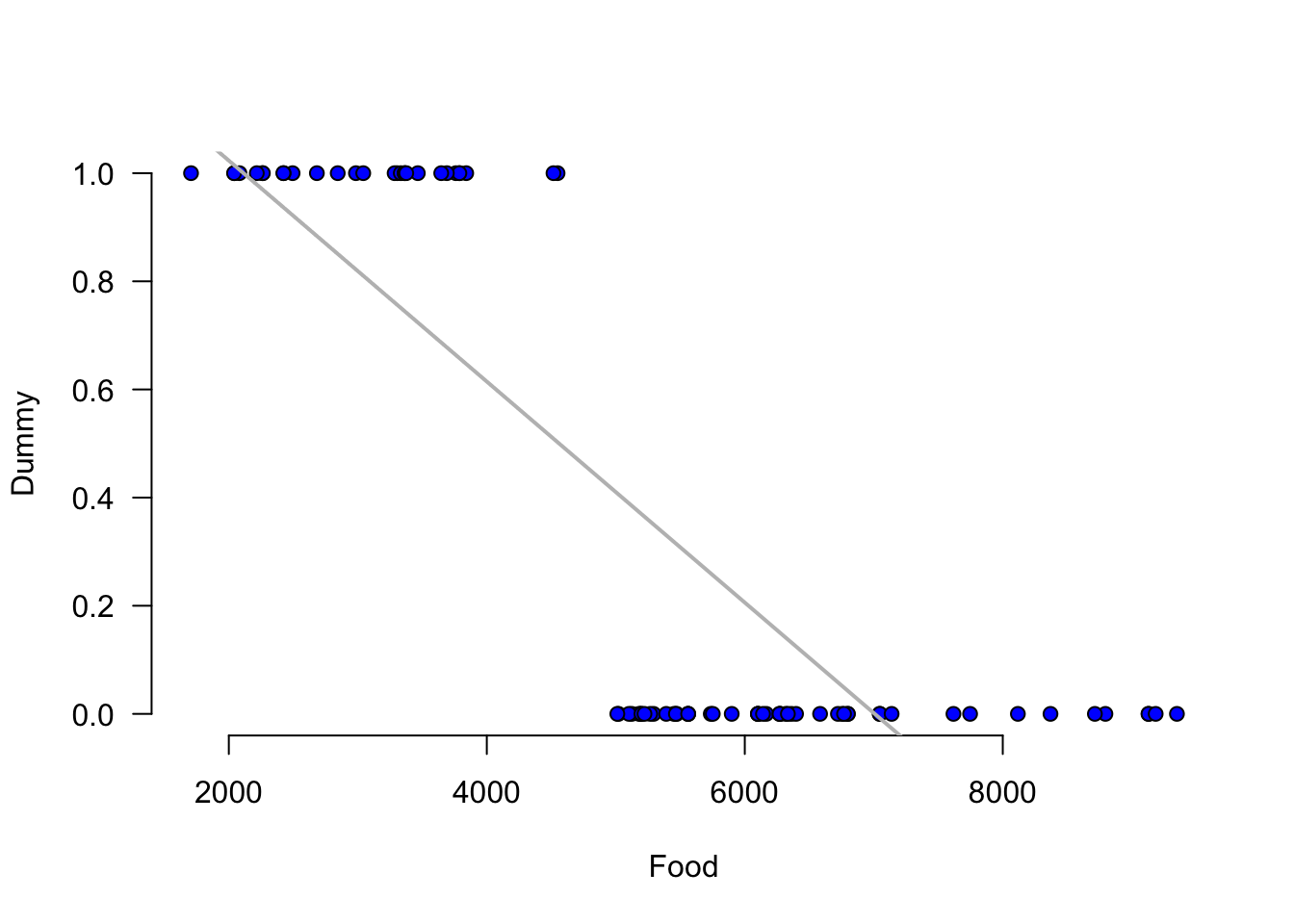

Exercise 4

  1. If we follow the \(R^2=0.81\) the model fits the data very well.

Let’s load the data from the web:

Population<-read.csv("https://jagelves.github.io/Data/Population.csv")

Now let’s filter the data so that we can focus on the population for Japan.

library(dplyr)

Attaching package: 'dplyr'
The following objects are masked from 'package:stats':

    filter, lag
The following objects are masked from 'package:base':

    intersect, setdiff, setequal, union
Japan<-filter(Population,Country.Name=="Japan")

Next, we can run the regression of Population against the Year. Let’s also run the summary() function to obtain the fit and the coefficients.

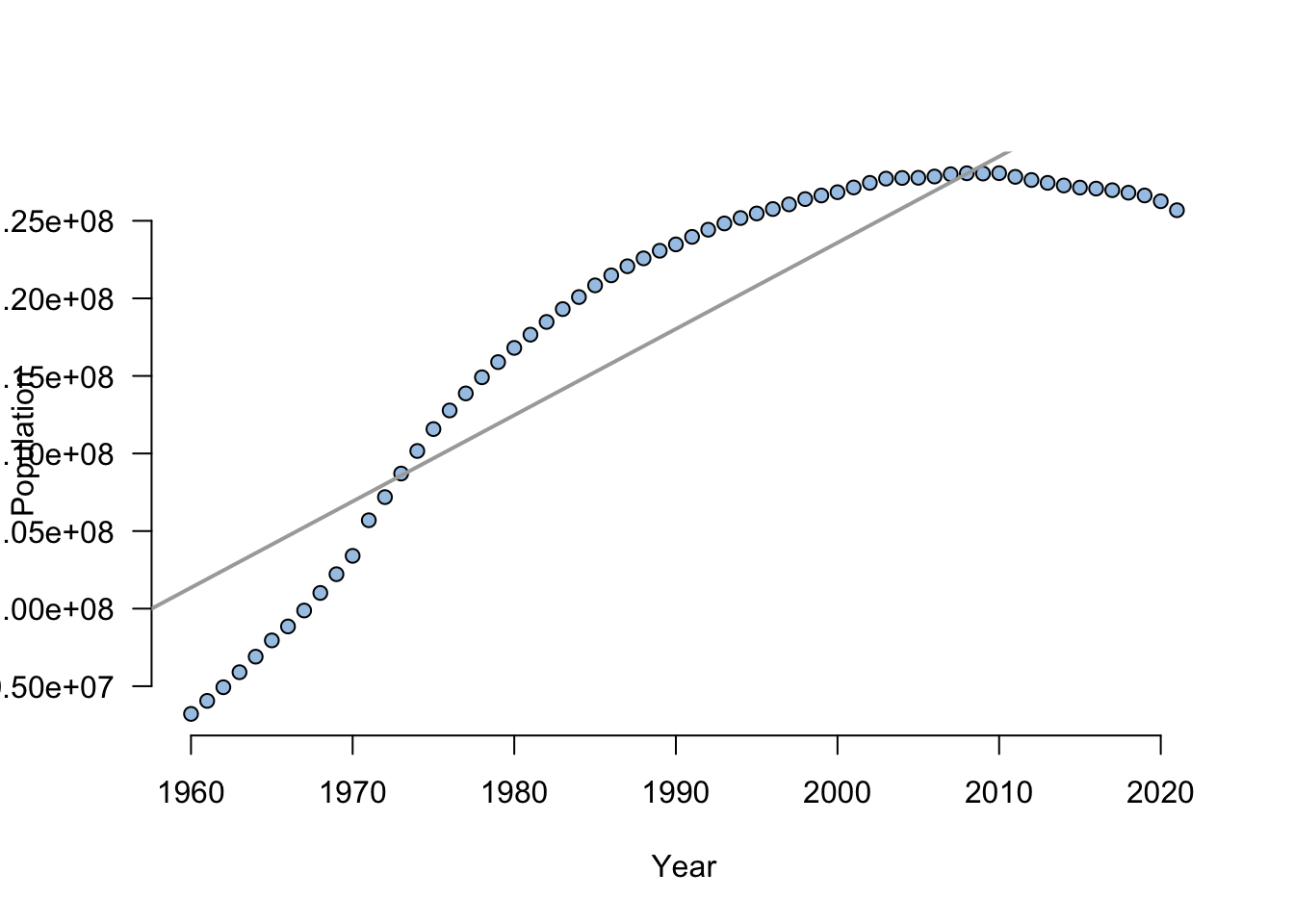
fit<-lm(Population~Year,data=Japan)
summary(fit)

Call:
lm(formula = Population ~ Year, data = Japan)

Residuals:
     Min       1Q   Median       3Q      Max 
-9583497 -4625571  1214644  4376784  5706004 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -988297581   68811582  -14.36   <2e-16 ***
Year            555944      34569   16.08   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4871000 on 60 degrees of freedom
Multiple R-squared:  0.8117,    Adjusted R-squared:  0.8086 
F-statistic: 258.6 on 1 and 60 DF,  p-value: < 2.2e-16
  1. The prediction for \(2030\) is about \(140\) million people.

Let’s use the predict() function:

predict(fit,newdata=data.frame(Year=c(2030)))
        1 
140268585
  1. After looking at the scatter plot, it seems unlikely that the population in Japan will hit \(140\) million. Population has been decreasing in Japan!

Use the plot() and abline() functions to create the figure.

plot(y=Japan$Population,x=Japan$Year, main="", 
     axes=F,pch=21, bg="#A7C7E7",
     xlab="Year",
     ylab="Population")
axis(side=1, labels=TRUE, font=1,las=1)
axis(side=2, labels=TRUE, font=1,las=1)
abline(fit,
       col="darkgray",lwd=2)