library(ISLR2)
table(BrainCancer$diagnosis)
Meningioma LG glioma HG glioma Other
42 9 22 14 2.1 Concepts
Frequency
A frequency distribution is a table/graph showing the number of items in each of several non-overlapping classes.
The relative frequency is calculated by \(f_{i}/n\), where \(f_{i}\) is the frequency of class \(i\) and \(n\) is the total frequency.
The cumulative frequency shows the number of data items in a class and all classes below.
The cumulative relative frequency is given by \(cf_{i}/n\), where \(cf_{i}\) is the cumulative frequency of class \(i\).
A contingency table classifies outcomes for one variable in rows and the other in columns. The values at the row and column intersections are frequencies for each unique combination of the two variables.
Plots
A bar plot illustrates the frequency distribution of qualitative data.
Is an illustration for qualitative data.
Includes the classes in the horizontal axis and frequencies or relative frequencies in the vertical axis.
Has gaps between each bar.
A pie chart illustrates the frequency distribution with a circle.
Each slice of the circle represents a class.
The size of each slice if proportionate to the size of the class.
All slices must represent a single class in the frequency distribution. Hence, all slices add up to make the circle.
A histogram illustrates the frequency distribution of quantitative data.
Is an illustration for quantitative data.
There are no gaps between the bars.
The number, width and limits of each class must be determined.
- The number of classes can be determined by the \(2^k\) rule: select \(k\) such that \(2^k\) is greater than the number of observations by the smallest amount.
- The width of the class is approximately range/(# of Classes). The value should be rounded up.
- The limits should be chosen so that each point belongs to only one class.
Useful R Functions
The table() command generates frequency distributions or contingency tables if two variables are used.
The prop.table() command generates relative frequency distributions from an object that contains a table.
The cut() function generates class limits and bins used in frequency distributions (and histograms) for quantitative data.
Base R has the barplot() function for categorical variable, histogram() function for numerical data, and the plot() function for line charts or scatter plots. Below are some arguments that are helpful when plotting.
- main: used to set the plot’s title. The title should be entered as a character.
- col: used to set the color of the plot. Hex and RGB values are allowed as inputs. The color should be entered as a character.
- xlab and ylab: are used to set the labels for the \(x\) and \(y\) axis respectively. The labels should be entered as characters.
legend()is a function to customize the legend of a graph. This argument may be used with theplot(),barplot()orhistogram()functions.- x: used to set the location of the legend in the plotting area. Ex: “bottomleft”.
- legend: a vector specifying the legend names to be included.
- col: a vector specifying the color of each item in the legend.
2.2 Exercises
The following exercises will help you practice summarizing data with tables and simple graphs. In particular, the exercises work on:
Developing frequency distributions for both categorical and numerical data.
Constructing bar charts, histograms, and line charts.
Creating contingency tables.
Answers are provided below. Try not to peak until you have a formulated your own answer and double checked your work for any mistakes.
Exercise 1
Install the ISLR2 package in R. You will need the BrainCancer data set to answer this question.
- Construct a frequency and relative frequency table of the Diagnosis variable. What was the most common diagnosis? What percentage of the sample had this diagnosis?
- Construct a bar chart. Summarize the findings.
- Construct a contingency table that shows the Diagnosis along with the Status. Which diagnosis had the highest number of non-survivals (0)? What was the survival rate of this diagnosis?
- Construct a stacked column chart. Which two Diagnosis and Status combinations are the most frequent?
Exercise 2
You will need the airquality data set (in base R) to answer this question.
- Construct a frequency distribution for Temp. Use five intervals with widths of \(50<x\le60\); \(60<x\le70\); etc. Which interval had the highest frequency? How many times was the temperature between \(50\) and \(60\) degrees?
- Construct a relative frequency, cumulative frequency and the relative cumulative frequency distributions. What proportion of the time was Temp between \(50\) and \(60\) degrees? How many times was the Temp \(70\) degrees or less? What proportion of the time was Temp more than \(70\) degrees?
- Construct the histogram. Is the distribution symmetric? If not, is it skewed to the left or right?
Exercise 3
You will need the Portfolio data set from the ISLR2 package to answer this question.
- Construct a line chart that shows the returns over time for each portfolio (X and Y) by using two lines each with a unique color. Assume the data is for the period \(1901\) to \(2000\). Include also a legend that matches colors to portfolios.
2.3 Answers
Exercise 1
- The most common diagnosis is Meningioma, a slow-growing tumor that forms from the membranous layers surrounding the brain and spinal cord. The diagnosis represents about \(48.28\)% of the sample.
Start by loading the ISLR2 package. To construct the frequency distribution table, use the table() function.
The relative frequency distribution can be easily retrieved by saving the frequency table in an object and then using the prop.table() function.
freq<-table(BrainCancer$diagnosis)
prop.table(freq)
Meningioma LG glioma HG glioma Other
0.4827586 0.1034483 0.2528736 0.1609195 - The majority of diagnosis are Meningioma. Low grade glioma is the least common of diagnosis. High grade glioma and other diagnosis have about the same frequency.
To construct the bar chart use the barplot() function in R.
barplot(freq, col = "#F5F5F5", ylim=c(0,50))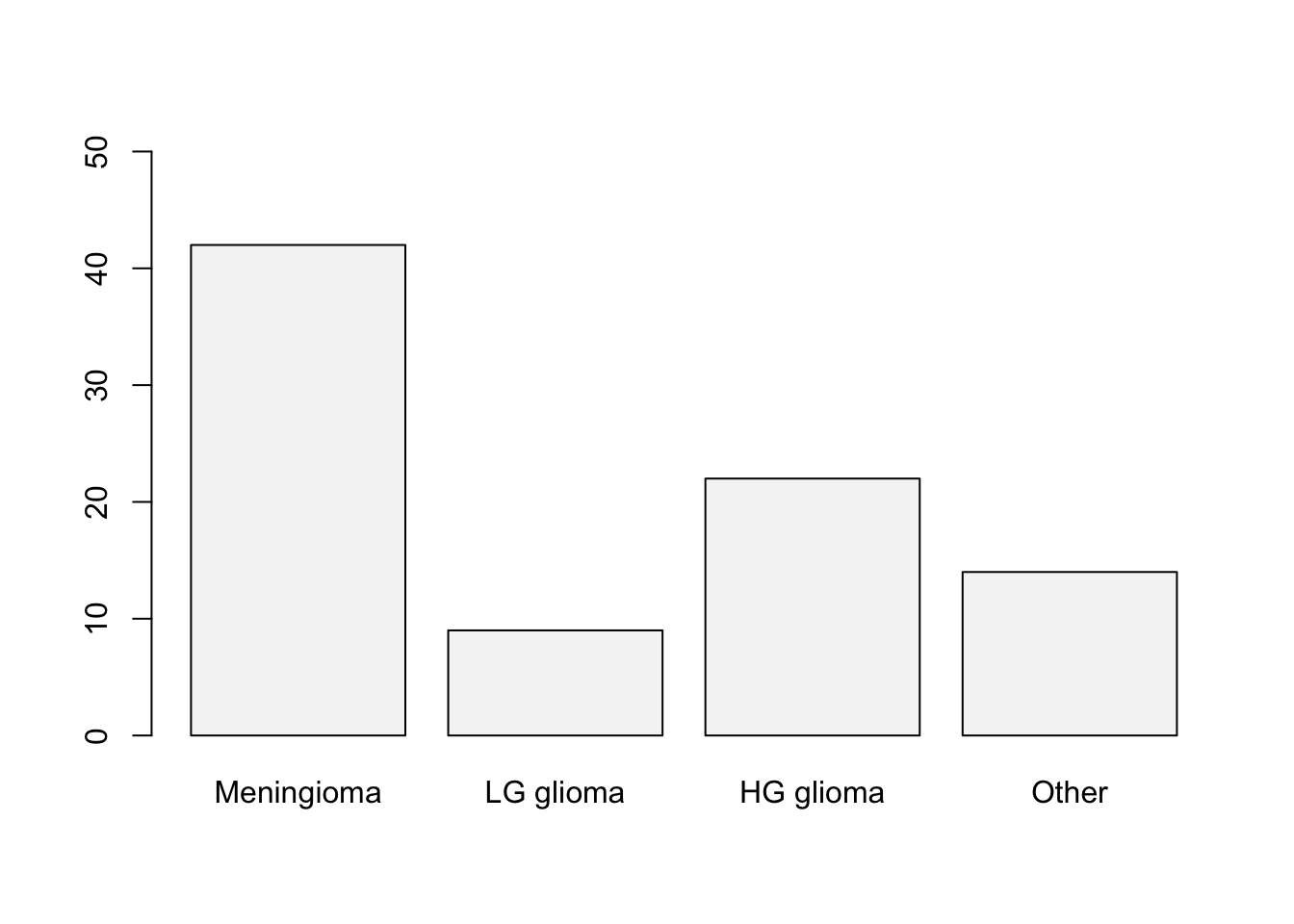
If you wish to use ggplot(), load the tidyverse package and use the geom_bar() function.
library(tidyverse)
ggplot(data=BrainCancer) +
geom_bar(aes(x=diagnosis),
fill="#F5F5F5",
col="black") +
labs(x="", y="Frequency")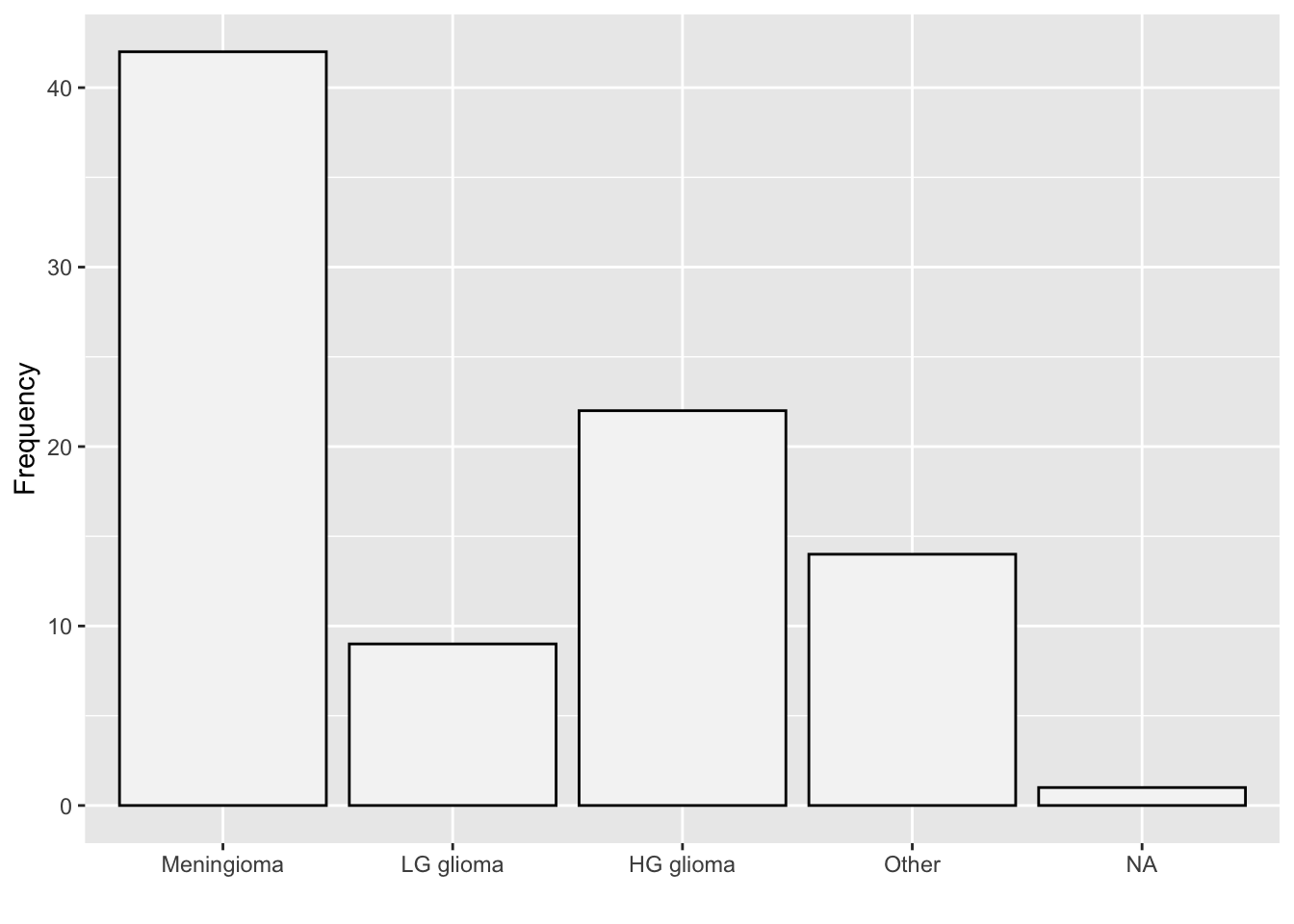
- \(33\) people did not survive Meningioma. The survival rate of Meningioma is only \(21.43\)%.
Use the table() function one more time to create the contingency table for the two variables.
(freq2<-table(BrainCancer$status,BrainCancer$diagnosis))
Meningioma LG glioma HG glioma Other
0 33 5 5 9
1 9 4 17 5To get the survival rates, we can use the prop.table() function once again.
prop.table(freq2,margin = 2)
Meningioma LG glioma HG glioma Other
0 0.7857143 0.5555556 0.2272727 0.6428571
1 0.2142857 0.4444444 0.7727273 0.3571429- Meningioma and not surviving is the most common with \(33\) occurrences. High grade glioma and surviving is the the second most common.
Use the barplot() function one more time to construct the stacked column chart.
barplot(table(BrainCancer$status,BrainCancer$diagnosis),
legend.text = c("Not Survived","Survived"), ylim=c(0,50))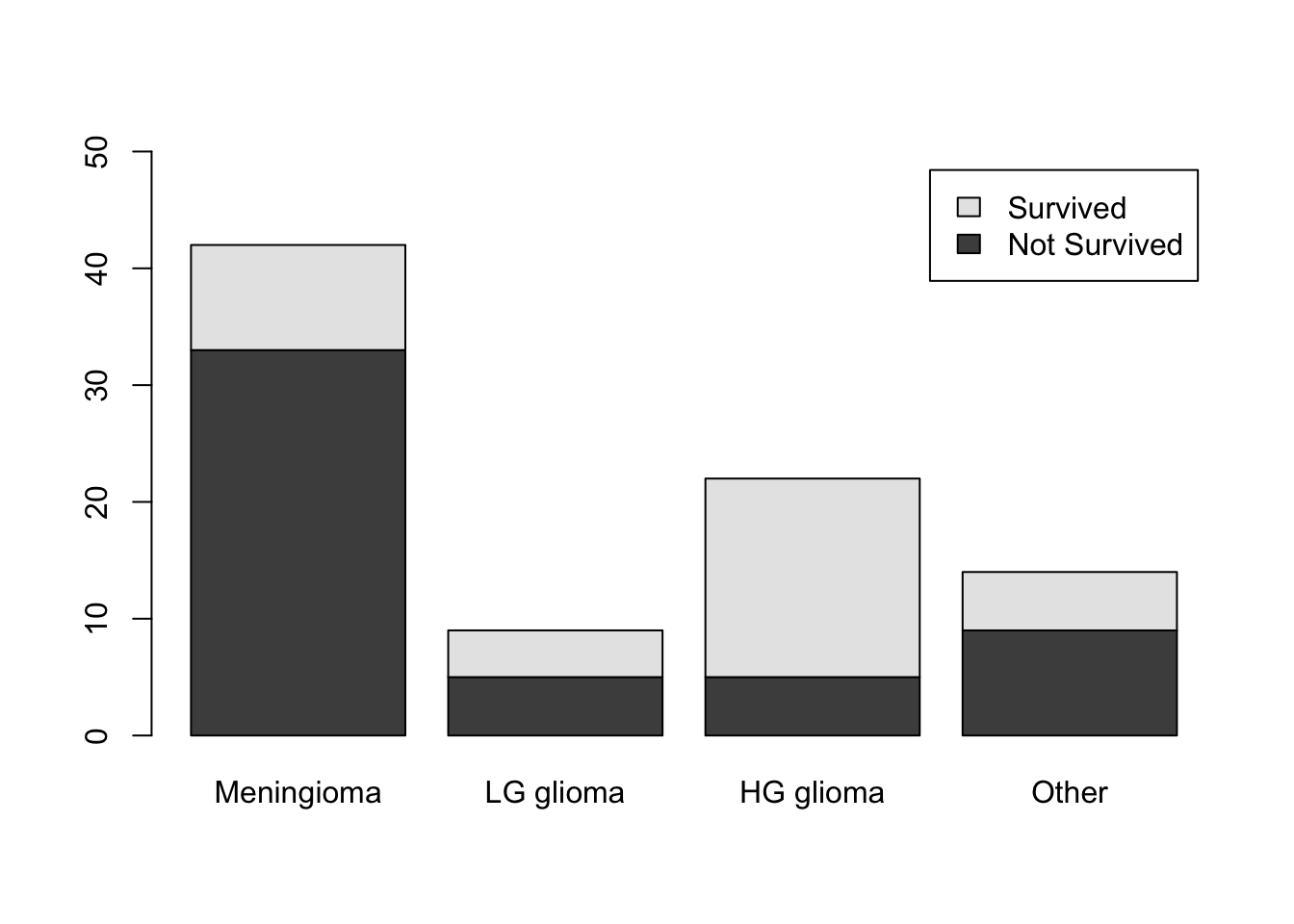
Exercise 2
- The highest frequency is in the \(80 < x ≤ 90\) bin. \(8\) temperatures were between \(50 < x ≤ 60\) degrees.
Create a vector containing the intervals desired by using the seq() function.
intervals <- seq(50, 100, by=10)Next use the cut() function to create the cuts for the histogram.
intervals.cut <- cut(airquality$Temp, intervals, left=FALSE, right=TRUE)The frequency distribution can be obtained by using the table() function on the interval.cut object created above.
table(intervals.cut)intervals.cut
(50,60] (60,70] (70,80] (80,90] (90,100]
8 25 52 54 14 - The temperature was \(5.22\)% of the time between \(50\) and \(60\); The temperature was \(70\) or less \(33\) times; The temperature was above \(70\), \(78.43\)% of the time.
To get the relative frequency table, start by saving the proportion table into an object.Then you can use the prop.table() function.
freq<-table(intervals.cut)
prop.table(freq)intervals.cut
(50,60] (60,70] (70,80] (80,90] (90,100]
0.05228758 0.16339869 0.33986928 0.35294118 0.09150327 For the cumulative distribution you can use the cumsum() function on the frequency distribution.
cumulfreq<-cumsum(freq)
cumulfreq (50,60] (60,70] (70,80] (80,90] (90,100]
8 33 85 139 153 Lastly, for the relative cumulative distribution table, you can use the cumsum() function on the relative frequency table.
cumsum(prop.table(freq)) (50,60] (60,70] (70,80] (80,90] (90,100]
0.05228758 0.21568627 0.55555556 0.90849673 1.00000000 - The distribution is not perfectly symmetric. It is skewed slightly to the left (see histogram.)
Use the hist() function to create the histogram.
hist(airquality$Temp, breaks=intervals,
right=TRUE,col="#F5F5F5", main="Temperature in NY", xlab="")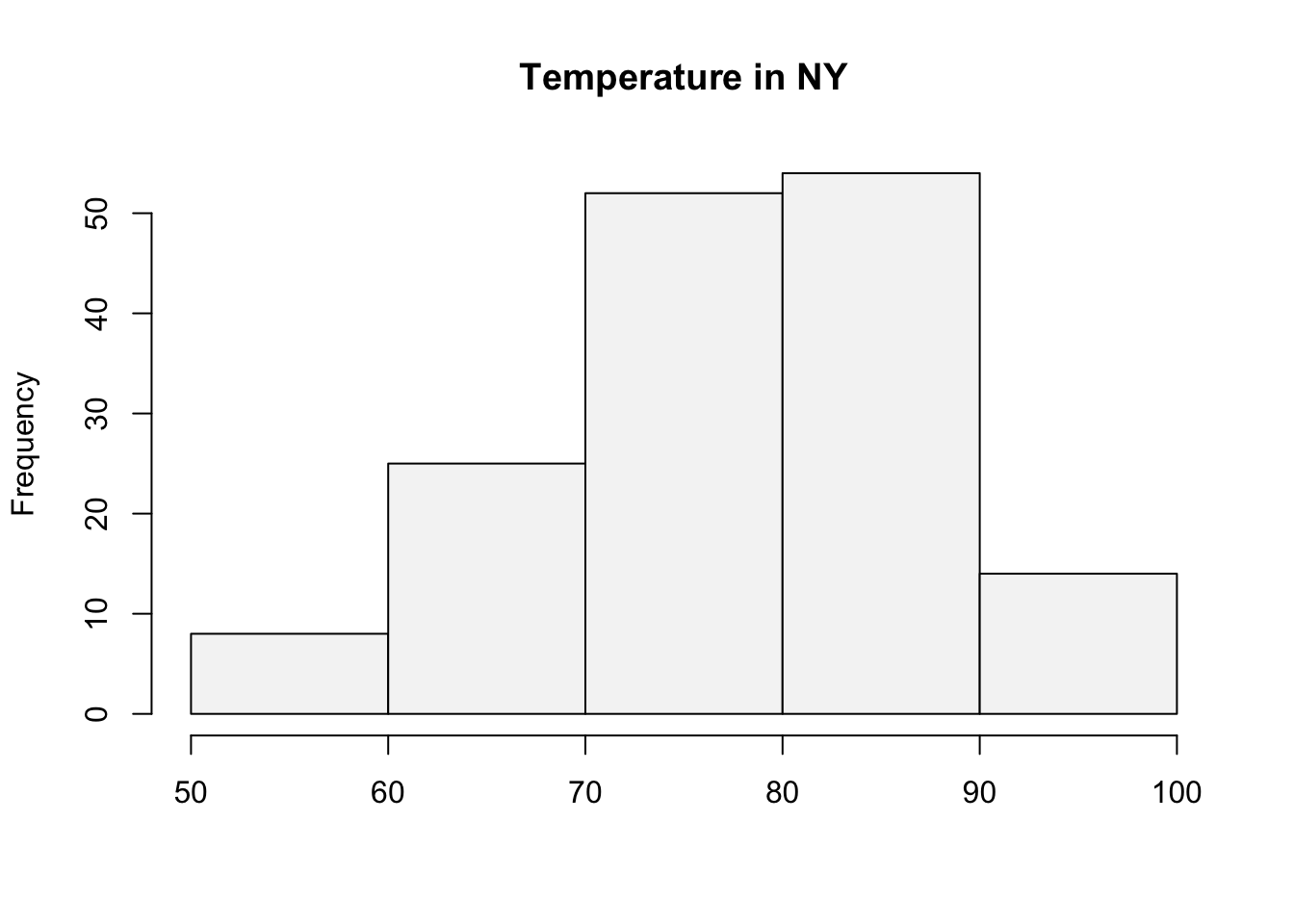
Alternately, the histogram may be constructed with ggplot using the code below:
library(ggthemes)
ggplot(data=airquality) +
geom_histogram(aes(x=Temp),
fill="grey",
alpha=0.6,
bins=5,col="black",
binwidth=10,
boundary=10) +
theme_clean()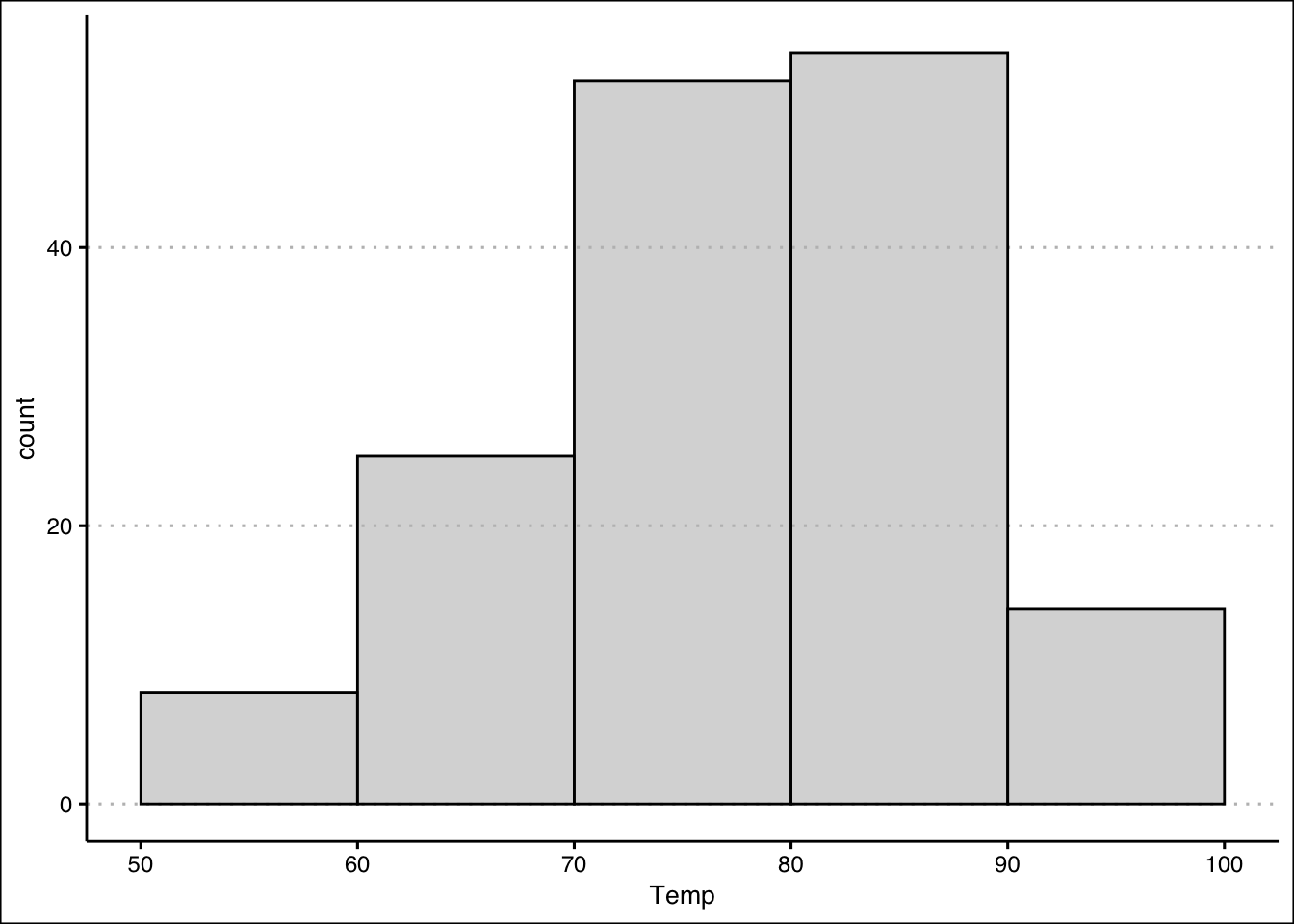
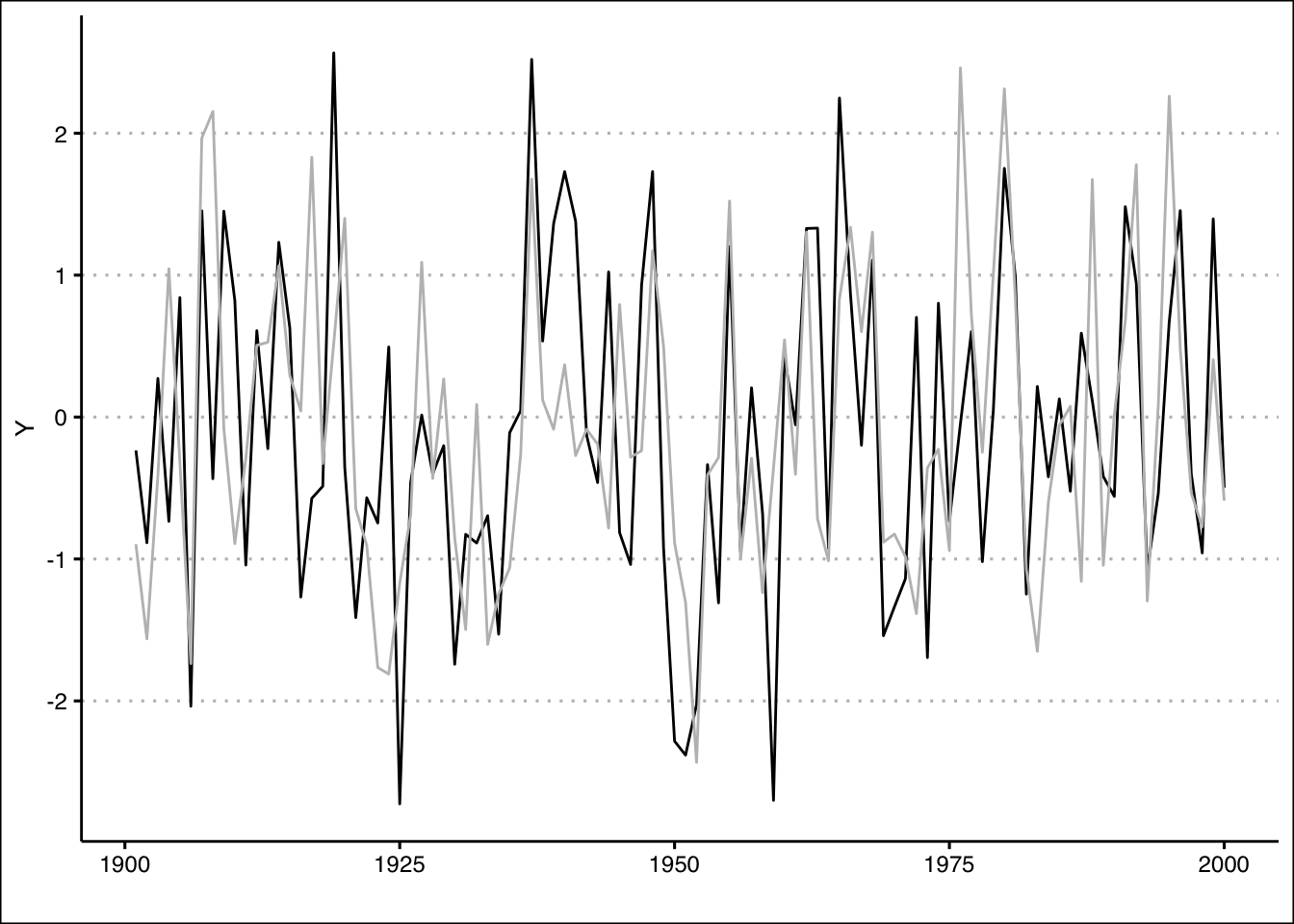
Exercise 3
- From \(1901\) through \(2000\), both portfolios have behaved very similarly. Returns are between \(-3\)% and \(3\)%, there is no trend, and positive (negative) returns for X seem to match with positive (negative) returns of Y.
You can use the plot() function to create a plot of Portfolio Y. The line for Portfolio X can be added with the lines() function.
plot(Portfolio$Y,
x=seq(1901,2000), type="l",
col="black", xlab="", ylab="% Return", ylim=c(-3,3),
xlim=c(1901,2000), lwd=2, axes = F)
axis(side=1, labels=TRUE, font=1,las=1)
axis(side=2, labels=TRUE, font=1,las=1)
lines(Portfolio$X, x=seq(1901,2000), type="l",
col="darkgrey", lwd=2)
legend(x = "bottomleft",
legend = c("Port Y", "Port X"),
lty = c(1, 1),
col = c("black", "darkgrey"),
lwd = 2,
bty="n")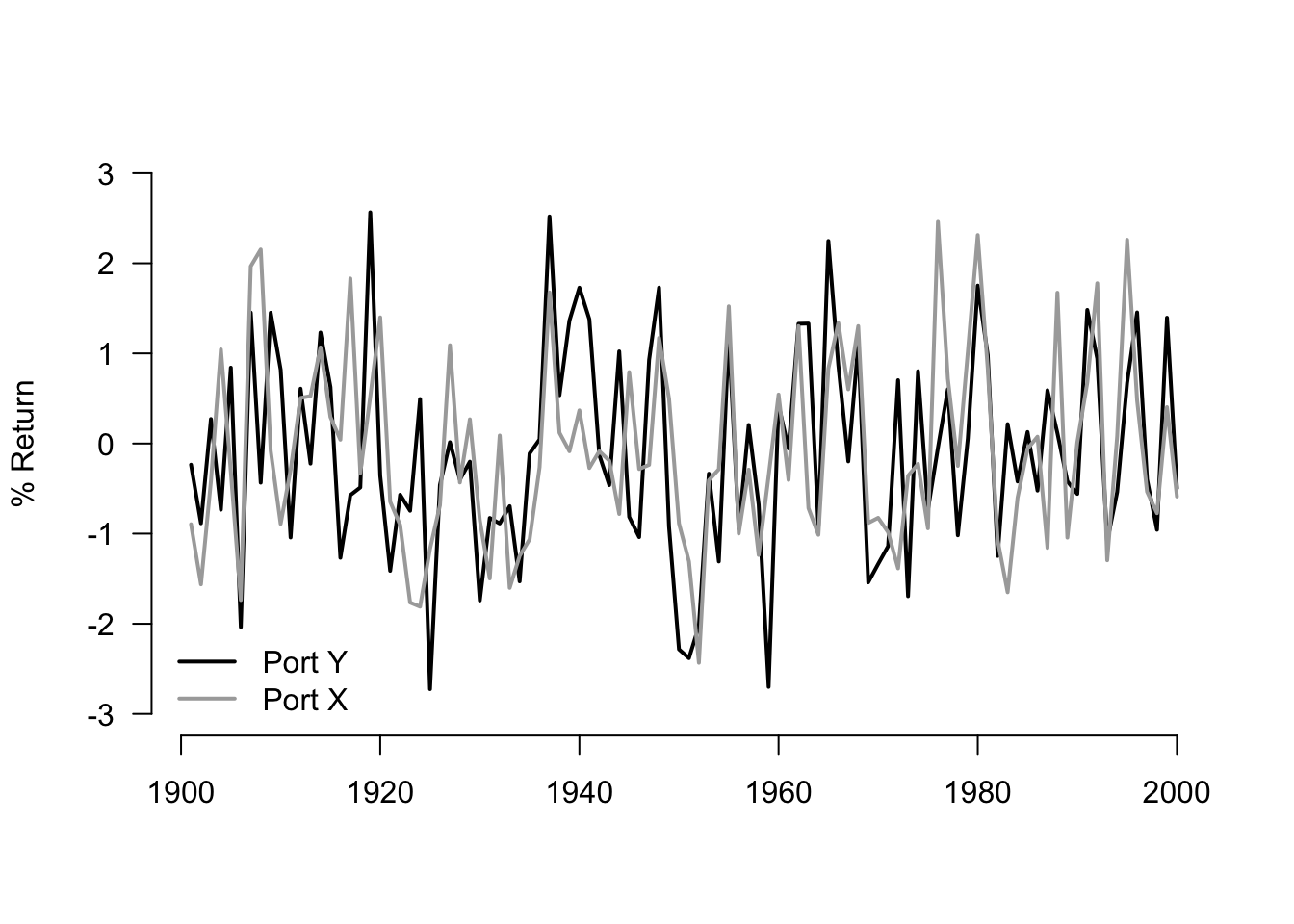 
We can once more recreate the plot using ggplot:
ggplot(data=Portfolio) +
geom_line(aes(y=Y, x=1901:2000),col="black") +
geom_line(aes(y=X, x=1901:2000),col="grey") +
labs(x="")+
theme_clean()